Join Our Groups
TOPIC 3: THREE DIMENSIONAL FIGURES
Sometimes before you make any purchases you may want to know for example, how much cloth you need to make a pillow cover. What about a cover for your mattress or sofa cushion? How much oil paint do you need to paint your drinking water tank?
What about the amount of cloth for the pocket covers of your radio, curtain, suit, gown, trousers, set of table clothes, etc.
Answers to such questions and of the kind leads you to think more carefully about the size of the surfaces (faces) to be covered or coated on the bodies at work. Perhaps you need to take some measurements on the surfaces.
The knowledge of the surface areas of such bodies will enable you to choose or purchases the required amount without unnecessary wastage so as to minimize purchases costs too.
Three Dimensional Figures
Classify three dimensional figures
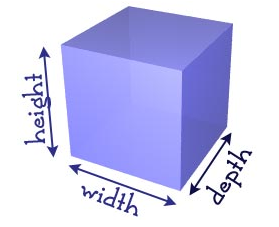
Three‐dimensional objects are the solid shapes you see every day, like boxes, balls, coffee cups, and cans.
It is called three-dimensional or 3D because there are three dimensions: width, depth and height.
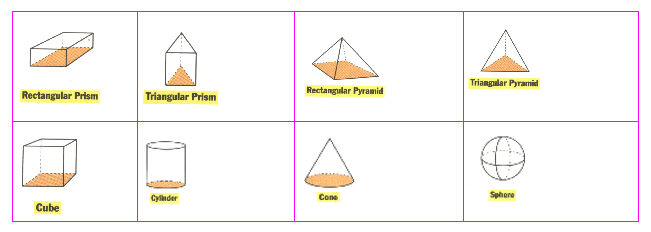
-The following table shows examples of some common three dimensional figures
The Characteristics of Each Class
List the characteristics of each class
Here are some helpful vocabulary terms for solids:
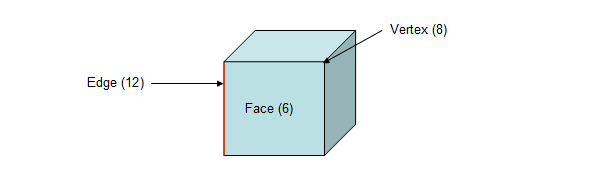
Base: Is the bottom surface of a solid object.
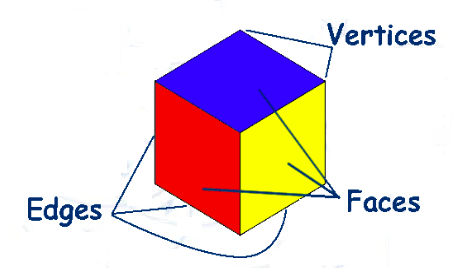
Edge: Is the intersection of two faces on a solid object. This is a line.
Face: Is a flat side of a 3‐dimensional object.
Prism: Is a solid object with two congruent and parallel faces.
Vertex: This is a point where three or more edges meet
Pyramid: Is a solid object with a polygon for a base and triangles for sides.
Three Dimensional Figures
Sketch three dimensional figures
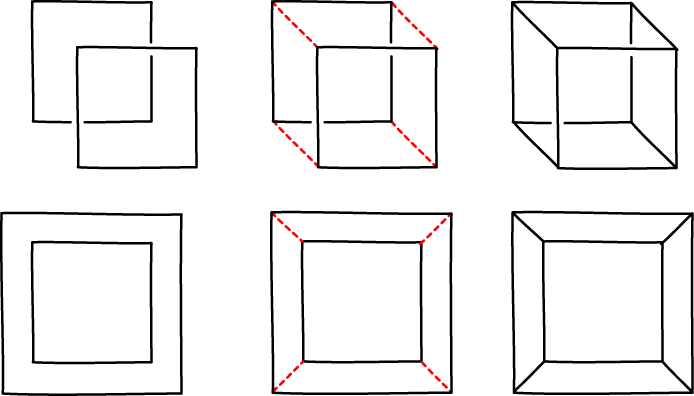
There are several ways of doing the drawing that corresponds to looking at the cube from different angles. The figure shows two ways of doing it.
Properties of Three Dimensional Figures
Identify properties of three dimensional figures
Three dimensional shapes have many attributes such as faces, edges andvertices. The flat surfaces of the 3D shapes are called the faces. The line segment where two faces meet is called an edge. Avertex is a point where 3 edges meet.
The Angle Between a Line and a Plane
Find the angle between a line and a plane
In finding the angle between the line and a plane in a three dimensional geometry, we use the right angled triangle. Joining the line to define the angle between the line and the plane that provides the least possible angle. Also, projection of one line to another on the plane is mostly used.
Example 1
For the pyramid VABCD with VA=VB=VC=VD=5m, and ABCD a square of side 4cm; find the angle between VA and ABCD.
Solution
Calculated by dropping a perpendicular from V to ABCD. This meets ABCD at X, the centre of the square.
So the projection of VA on ABCD is AX. AC= square root of (AB2 +BC2) =square of 42+42 =square root of 32. AX =1/2square root of32. cos (1/2square root 32)/5=0.5657, so VAX is 55.6.
The Angle Between Two Planes
Calculate the angle between two planes
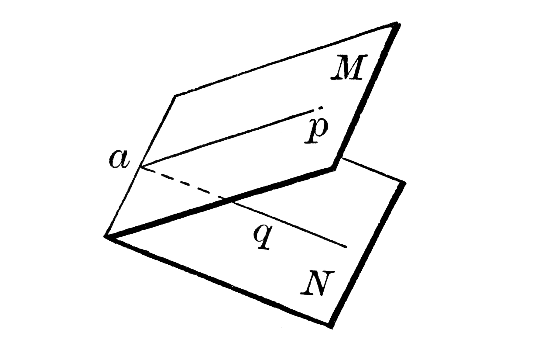
There are infinite possible lines that could be drawn on planes, making different angles with each other. The angle between planes is the angle between lines within those planes, Must be the lines which are at the middle of the plane for non rectangular planes and any other lines for rectangular planes. Then Right angled triangles are used to find the angles between those planes.
Example 2
In the diagram given below two planes M and N meet at ‘a’ forming the angle PAQ, this angle PAQ formed when these two planes meet is the angle at ‘a’ between the planes where lines pa cross line qa.
The Formulae for Calculating the Surface Area of Prisms, Cylinder and Pyramids and Cone
Derive the formulae for calculating the surface area of prisms, cylinder and pyramids and cone
Surface Area of a Right Circular Cone
A right circular cone is a cone whose vertex is vertically above the centre of the base of the cone.
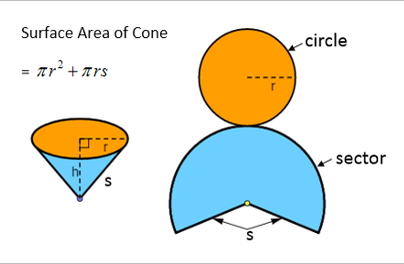
Area of circular base =Πr2 (it is an area of a circle)
and the area of the sector (which is part of the part of a circle of radius ‘s’ and arc length (same as circumferance of the base) =2πr) = πs2 x r/s = πrs
Therefore the total surface area of a right circular cone =Πr2 +Πrs = Πr (r + s)
Example 3
Find the total surface of right circular cone whose slant light is 10cm and whose base radius is 8cm.Use Πr(r +s)
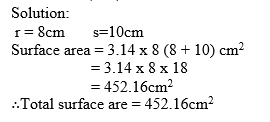
Example 4
Find the total surface area of a cone with diameter 8m and slant height of 10m. Use Π= 3.14
Surface Area of A Right Cylinder
If you want to know the amount of the covering the surface of a blue band margarine can, then you are finding the surface area of a right cylinder. Total surface area of the can is the sum of the areas of the top and bottom. Circular surfaces plus the area of the curved surface,
Now, consider a right cylinder of radius r and height h.
If the cylinder is opened up, the curved surface flattens out to form a rectangle. The length of the rectangle is 2Πr(the circumference of the circular base) and the width is h (the height of the cylinder).
Total surface area of cylinder:
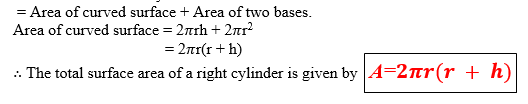
Example 5
Find the total surface area of a cylinder with radius of 3m and height of 10m. Use Π= 3.14
Surface Area of a Right Pyramid
A right pyramid is one in which the slant edges joining the vertex to the corner of the base are equal
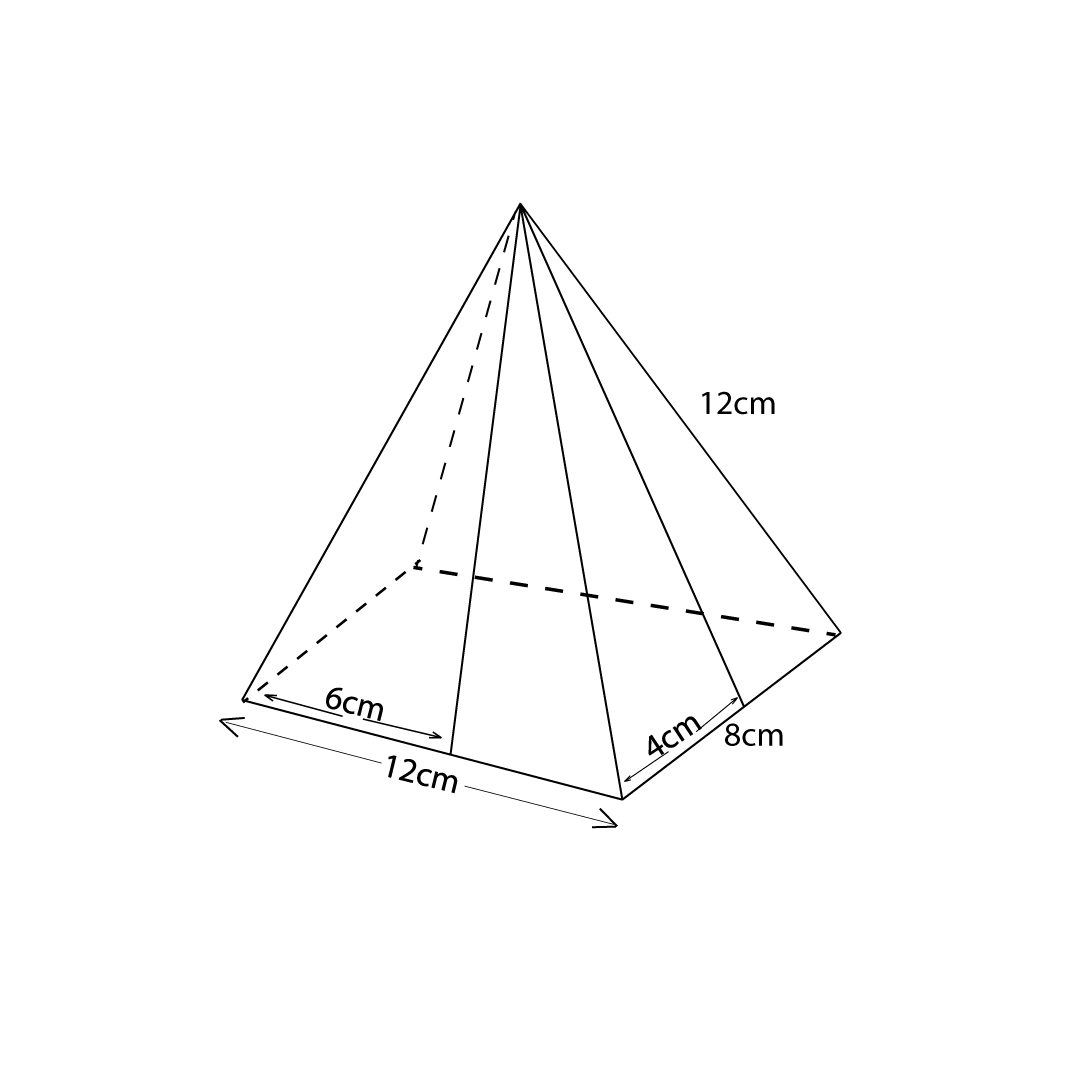
Example 6
A right rectangular pyramid is such that the rectangle is 12cm by 8cm and each slant edge is 12cm. Find the total surface area of the pyramid.
Surface Area of a Right Prism
A full brick or concrete block is an example of a right rectangular prism
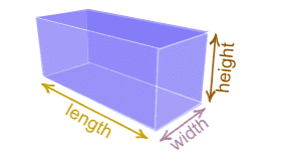
A right prism is a prism in which each of the vertical edges is perpendicular to the plane of the base.
The figure above shows a rectangular right prism in which there are 6 faces though only three of them can be seen easily.
Surface Area = Total or sum of the areas of each face.
Generally for any right prism,
Example 7
The height of a right prism is 4cm and the perimeter of its base is 30cm. Find the area of its lateral surface.
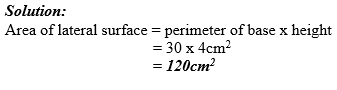
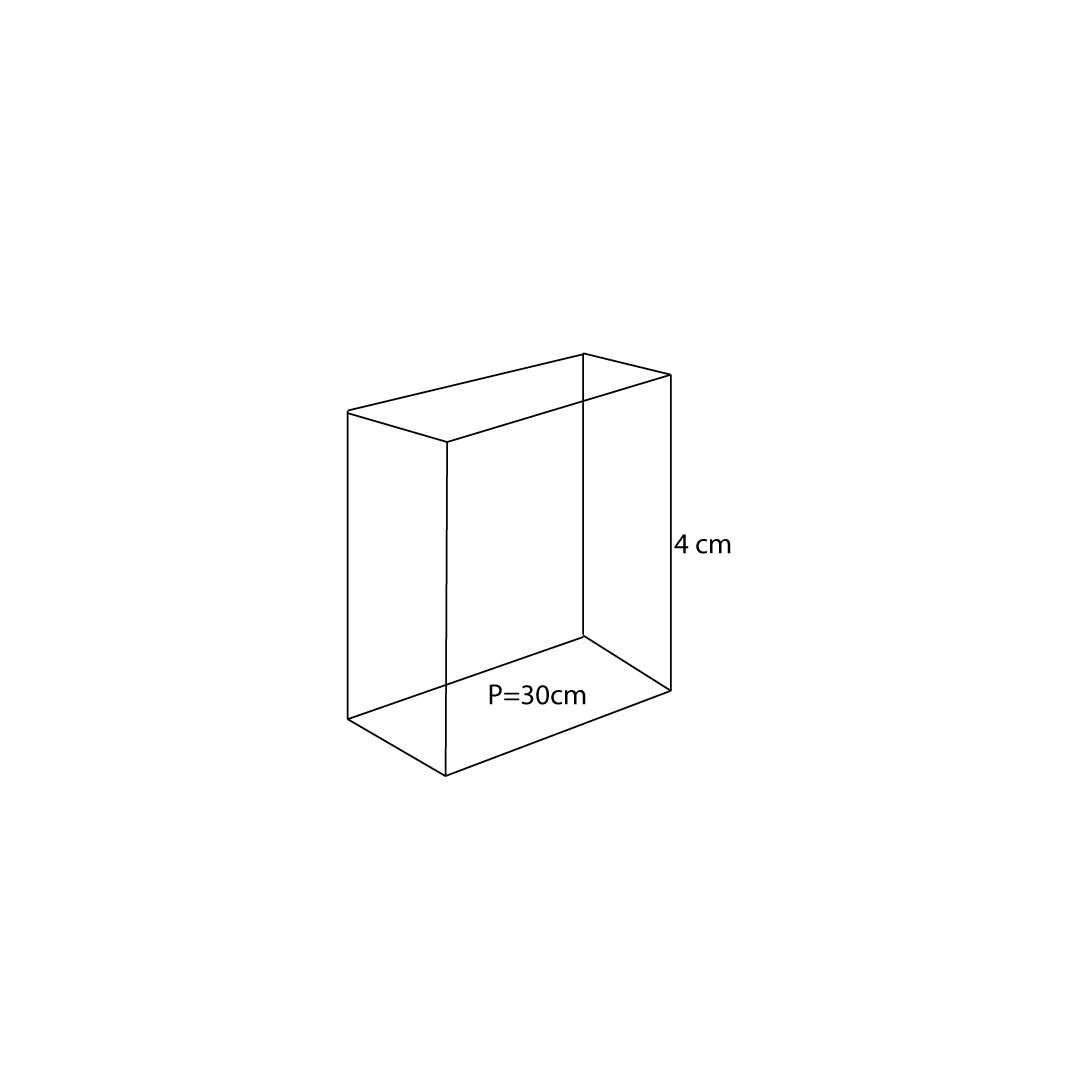
Example 8
Find the total surface area of a rectangular prism 12 by 8 by 6 cm high.
The Formulae to Calculate the Surface Area of Spheres
Apply the formulae to calculate the surface area of spheres
Surface Area of a Sphere
The figure above shows a sphere (ball) with radius “r”
The surface area of a sphere is four times the area of circle with the same radius. The area of a circle is Πr2. Hence, the surface area of sphere is equal to 4Πr2.
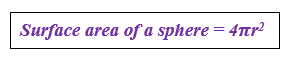
Example 9
Find the surface area of a sphere of radius 5cm. (Π= 3.14)
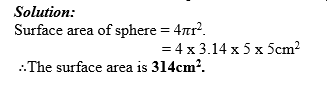
Example 10
Find the surface area of a tennis ball, given that its radius is 3.3cm. UseΠ= 3.14 Express your answer to the nearest tenth.
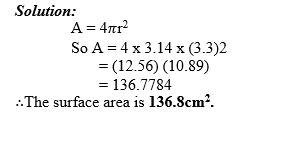
Exercise 1
Do the exercise to check your understanding. Use π= 3.14 throughout the exercise.
1.The altitude of a rectangular prism is 4cm and the width and lengths of its base are 2cm and 3cm respectively calculate the total surface area of the prism.
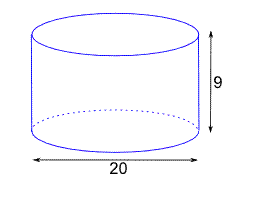
2. The following diagram shows a cylinder of diameter 20 units and height 9 units. What is its curved surface area?
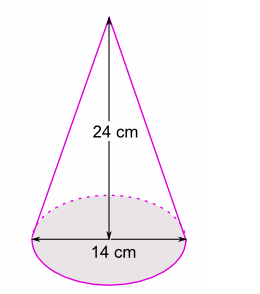
3. The diagram below shows a cone of height 24 cm and base diameter 14 cm. what is its total surface area?
4. The base of a right pyramid is a rectangle 6cm by 8cm and the slant edges are each 9cm long. Calculate its lateral surface area.
5. Find the total surface area of a circular cylinder of diameter 8cm and height 6cm.
6. Taking the earth to be a sphere with radius 6400km, find its surface area.
The Formulae for Calculating Volume of Prisms, Cylinders and Pyramids
Derive the formulae for calculating volume of prisms, cylinders and pyramids
VOLUMS OF SOME THREE – DIMENSIONAL FIGURES
We have seen some formulas for calculating the surface areas of some three dimensional figures.
Let us see as well formulas for calculating the volumes of such figures.
-The amount of space that is enclosed by a space figure is called the volume.
The Volume is measured in cubic units, cubic meters (m3), Cubic centimeters (cm3) etc.
When we find (calculate) the volume of a space figure or solid, we are finding the number of
cubic units enclosed by the given spaces figure.
(a) Volume of a Right Prism
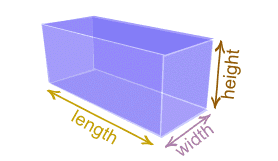
The figure above shows a right rectangular prism. Let h be height, w width and ɭ the length of the prism.
Then the Volume of the prism is given by: V = Base area x height= ɭ×W×h
Generally, volume of any right prism is equal to the product of the area of the base and the height V = Base area x height.
(b) Volume of a Right Cylinder
Consider a right circular cylinder with radius” r “and height h as shown below.
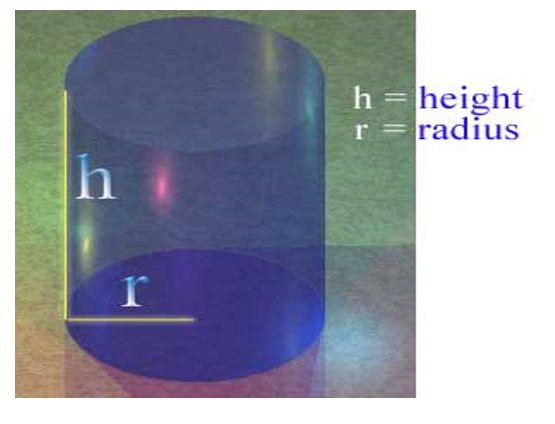
The volume of a right circular cylinder is equal to the product of the area of the base and the height.
If V is volume, A is area of the base and h is the height,
Then Volume = Area of base x height
(c) Volume of a Pyramid
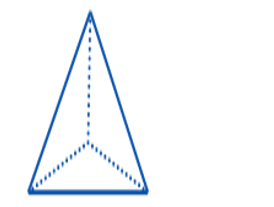
Generally, the volume of a pyramid is one – third the product of its altitude (height) and its base area.
If h is the perpendicular distance from the vertex of the pyramid to its base then,
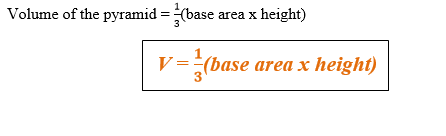
(d)Volume of a Cone
Consider a cone of radius “r” and altitude h as shown below.
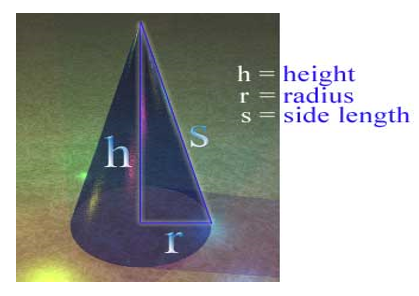
(e) Volume of a Sphere
The figure above shows a sphere of radius r, if the sphere can be put inside a cylinder of the same radius” r”, then the height h = 2r.
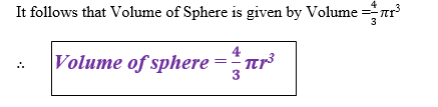
The Formulae to Calculate the Volume of Cylinders, Pyramids and Cones
Apply the formulae to calculate the volume of cylinders, pyramids and cones
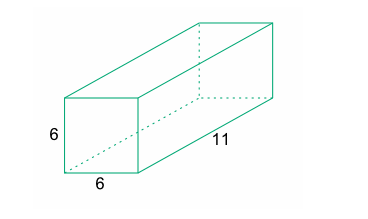
Example 11
Find the volume of the prism shown below, given that the dimensions are in meters (m)
Example 12
Calculate the volume of a rectangular prism whose base is 8cm by 5cm and whose height is 10cm.
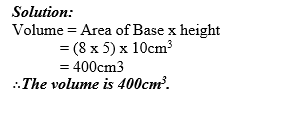
Example 13
Calculate the radius of a right circular cylinder of volume 1570m3 and height 20m. Use π=3.14
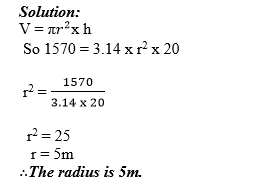
Example 14
A pipe made of metal 1cm thick, has an external (outside) radius of 6cm. Find the volume of metal used in making 4m of pipe. Use π=3.14
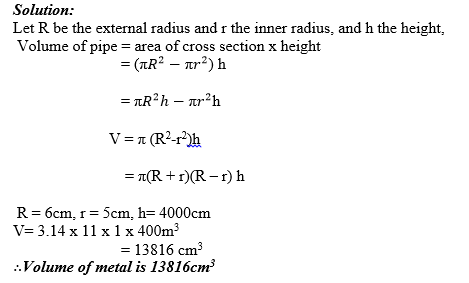
Example 15
Find the volume of a pyramid with rectangular base with length 6m and width 4m if the height of the pyramid is 10m.
Example 16
Calculate the volume of a square pyramid whose altitude is 10cm and length of side of base is 6cm.
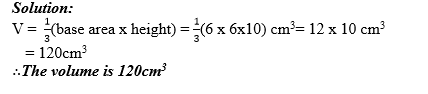
Example 17
Calculate the volume of a cone having base radius 10cm and altitude 12 cm Use π=3.14
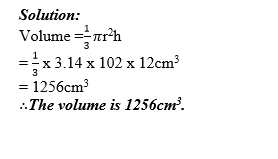
Example 18
Find the volume of a sphere whose radius is 10cm. (Take π= 3.14).
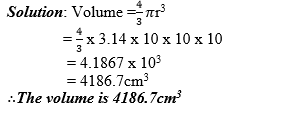
Example 19
The volume of a spherical tank is 268m3. Calculate the radius of the tank. (π= 3.14)
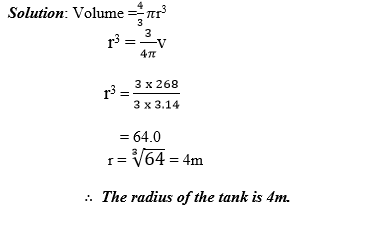
Example 20
Find the volume of rubber in a hollow spherical ball with inner diameter 14cm and outer diameter 16cm. (Take π = 3.14)
Exercise 2
Answer the following questions and (use π = 3.14)
1. What is the volume of a right prism whose base is a regular hexagon ( n = 6) with a side of the base 4cm long and the height of the prism.
2. Find the volume of a cylinder whose diameter is 28cm and whose height is 12cm.
3. Find the volume of a square pyramid whose height is 24cm and slant edge 25cm each.
4. The slant height of a cone is 20cm and the radius of its base is 12cm. Find its volume in terms of π.
5. The volume of a sphere is 827cm3. Find its radius.
6. A cylinder and sphere have the same volume. If the radius of the sphere is 5cm and radius of the cylinder is 3cm, Calculate height of the cylinder.
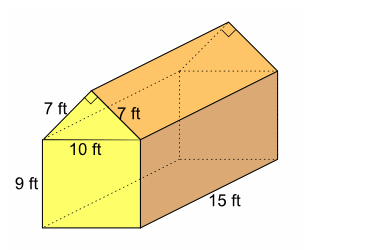
8.The diagram shows a barn. What is the volume of the barn? (The length of the hypotenuse in the right triangle is rounded to the nearest foot.)
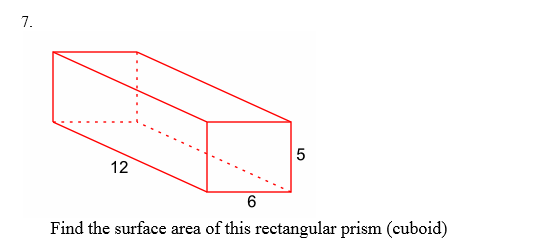
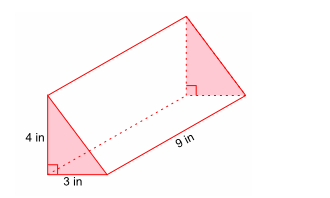
9.What is the volume of this prism?
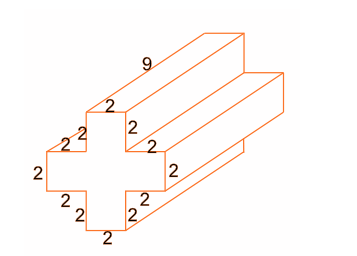
The diagram shows a prism whose cross-section is a right triangle. What is the volume of the prism?
Summary of the topic
Here are the important formulas you have covered under the section on surface areas summarized.
Surface area of:
You can now have a summary of the important formulas for calculating volume of some three dimensional figures as follows:-
Very good notes
返信削除