Join Our Groups
TOPIC 11: PERIMETERS AND AREAS
The Perimeters of Triangles and Quadrilaterals
Find the perimeters of triangles and quadrilaterals
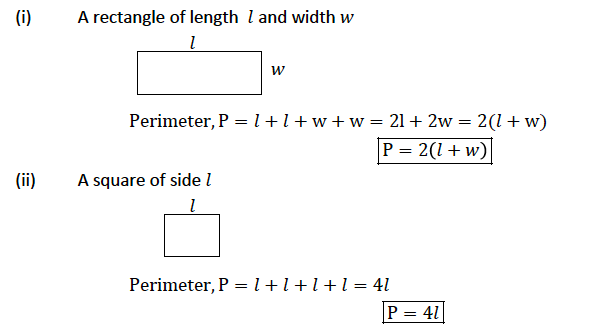
Perimeter – is defined as the total length of a closed shape. It is obtained by adding the lengths of the sides inclosing the shape. Perimeter can be measured in 𝑚𝑚 , 𝑐𝑚 ,𝑑𝑚 ,𝑚,𝑘𝑚 e. t. c
Examples
Example 1
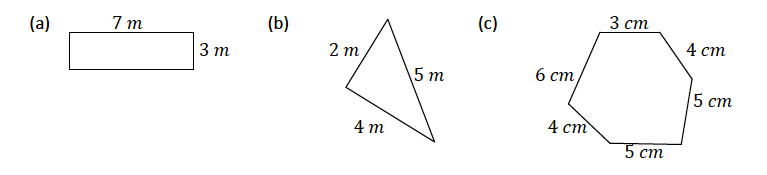
Find the perimeters of the following shapes
Solution
- Perimeter = 7𝑚 + 7𝑚 + 3𝑚 + 3𝑚 = 20 𝑚
- Perimeter = 2𝑚 + 4𝑚 + 5𝑚 = 11 𝑚
- Perimeter = 3𝑐𝑚 + 6𝑐𝑚 + 4𝑐𝑚 + 5𝑐𝑚 + 5 𝑐𝑚 + 4𝑐𝑚 = 27 𝑐𝑚
The Value of Pi ( Π)
Estimate the value of Pi ( Π)
The number π is a mathematical constant, the ratio of a circle's circumference to its diameter, commonly approximated as 3.14159. It has been represented by the Greek letter "π" since the mid 18th century, though it is also sometimes spelled out as "pi" (/paɪ/).
The perimeter of a circle is the length of its circumference 𝑖. 𝑒 𝑝𝑒𝑟𝑖𝑚𝑒𝑡𝑒𝑟 = 𝑐𝑖𝑟𝑐𝑢𝑚𝑓𝑒𝑟𝑒𝑛𝑐𝑒. Experiments show that the ratio of the circumference to the diameter is the same for all circles
The Circumference of a Circle
Calculate the circumference of a circle
Example 2
Find the circumferences of the circles with the following measurements. Take 𝜋 = 3.14
- diameter 9 𝑐𝑚
- radius 3½𝑚
- diameter 4.5 𝑑𝑚
- radius 8 𝑘𝑚
Solution
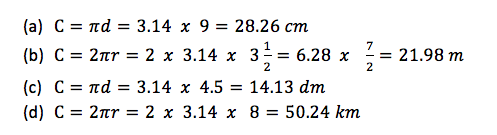
Example 3
The circumference of a car wheel is 150 𝑐𝑚. What is the radius of the wheel?
Solution
Given circumference, 𝐶 = 150 𝑐𝑚
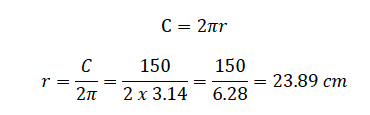
∴ The radius of the wheel is 23.89 𝑐𝑚
The Area of a Rectangle
Calculate the area of a rectangle
Area – can be defined as the total surface covered by a shape. The shape can be rectangle, square, trapezium e. t. c. Area is measured in mm!, cm!,dm!,m! e. t. c
Consider a rectangle of length 𝑙 and width 𝑤
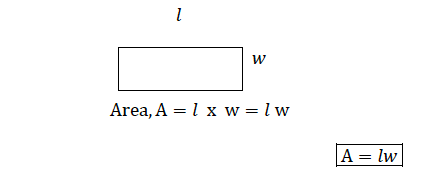
Consider a square of side 𝑙
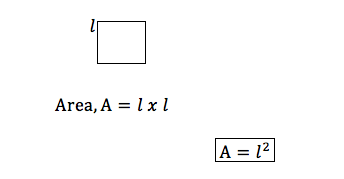
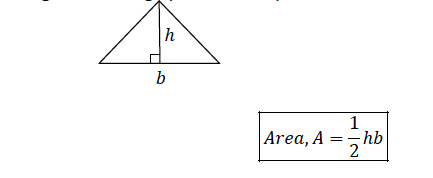
Consider a triangle with a height, ℎ and a base, 𝑏
The Area of a Parallelogram
Calculate area of a parallelogram
A parallelogram consists of two triangles inside. Consider the figure below:
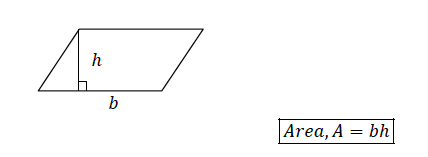
The Area of a Trapezium
Calculate the area of a trapezium
Consider a trapezium of height, ℎ and parallel sides 𝑎 and 𝑏
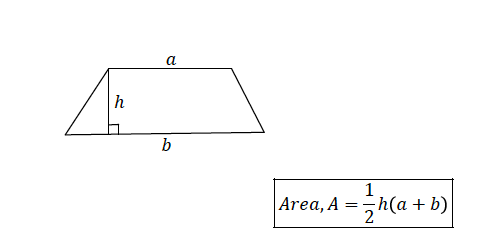
Example 4
The area of a trapezium is120 𝑚!. Its height is 10 𝑚 and one of the parallel sides is 4 𝑚. What is the other parallel side?
Solution
Given area, 𝐴 = 120 𝑚2, height, ℎ = 10 𝑚, one parallel side, 𝑎 = 4 𝑚. Let other parallel side be, 𝑏
Then
Areas of Circle
Calculate areas of circle
Consider a circle of radius r;
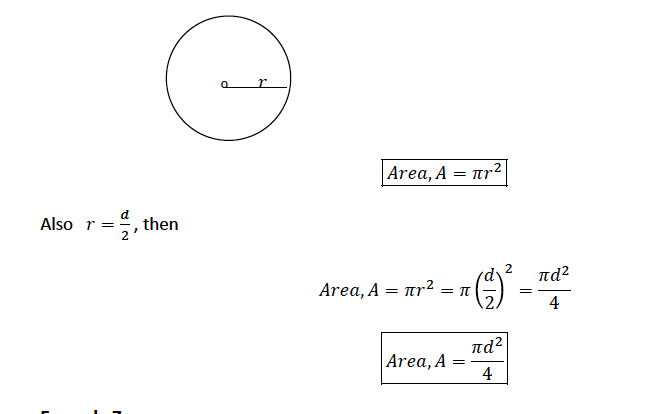
Example 5
Find the areas of the following figures
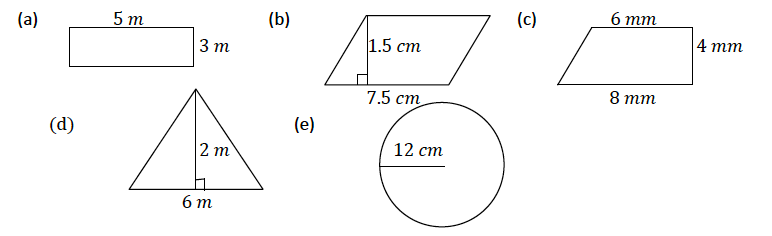
Solution
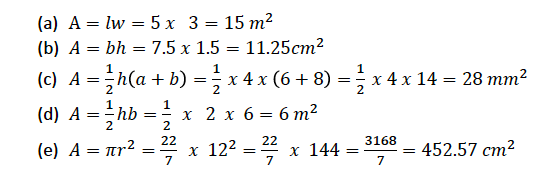
Example 6
A circle has a circumference of 30 𝑚. What is its area?
Solution
Given circumference, 𝐶 = 30 𝑚
C = 2𝜋𝑟
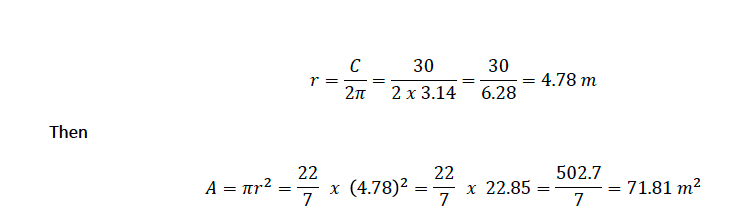
Exercise 1
1. The length of a rectangle is 6 cm, and the width is 4 cm. Find the perimeter and area of a rectangle.
2. Find the area of a circle with diameter 35 cm.( use Π = 22/7)
3. Calculate the area of a trapezium with parallel sides 3 cm and 5 cm and distance between them is 12 cm.
4. Find the height of a triangle with base 50 cm and area 300 cm2.
5. Find the area of a circle of diameter 40 cm. ( given π=3.14).
Thanks for notes
返信削除