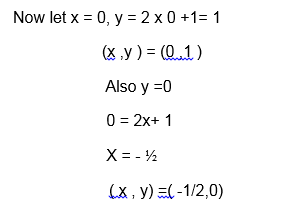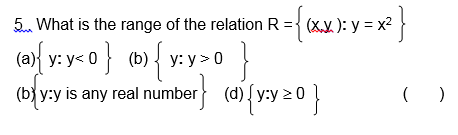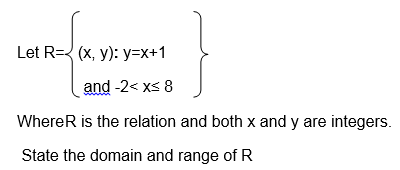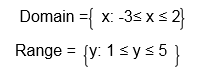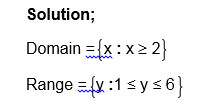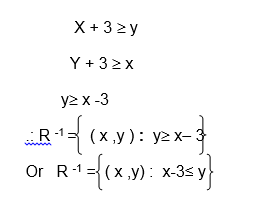JOIN US WHATSAPP
CLICK HERE
JOIN US TELEGRAM
CLICK HERE
TOPIC 1: RELATIONS
Normally relation deals with matching of elements from the first set called DOMAIN with the element of the second set called RANGE.
Relations
A relation “R” is the rule that connects or links the elements of one set with the elements of the other set.
Some examples of relations are listed below.
- “Is a brother of “
- “Is a sister of “
- “Is a husband of “
- “Is equal to “
- “Is greater than “
- “Is less than “
Normally relations between two sets are indicated by an arrow coming from one element of the first set going to the element of the other set.
Relations Between Two Sets
Find relations between two sets
The relation can be denoted as:
R = {(a, b): a is an element of the first set, b is an element of the second set}
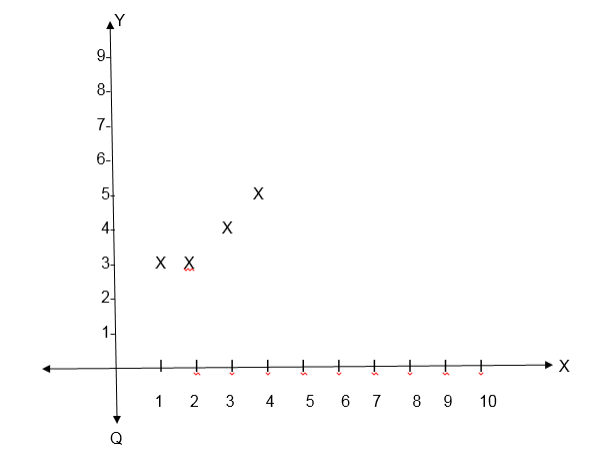
Consider the following table
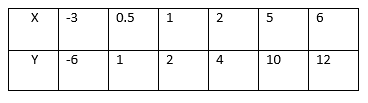
This is the relation which can be written as a set of ordered pairs {(-3, -6), (0.5, 1), (1, 2), (2, 4), (5, 10), (6, 12)}. The table shows that the relation satisfies the equation y=2x. The relation R defining the set of all ordered pairs (x, y) such that y = 2x can be written symbolically as:
R = {(x, y): y = 2X}.
Relations Between Members in a Set
Find relations between members in a set
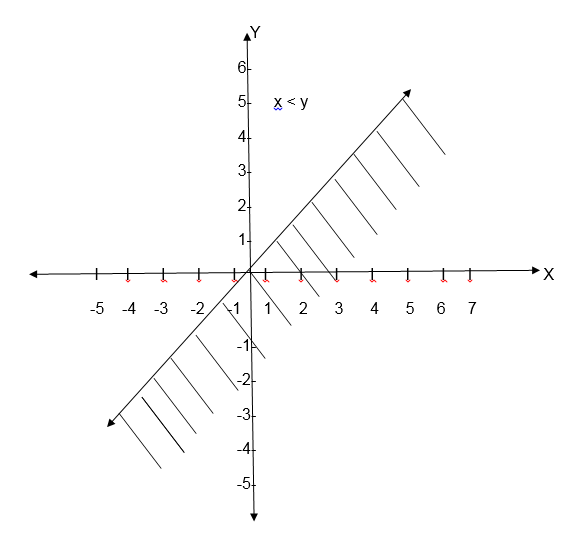
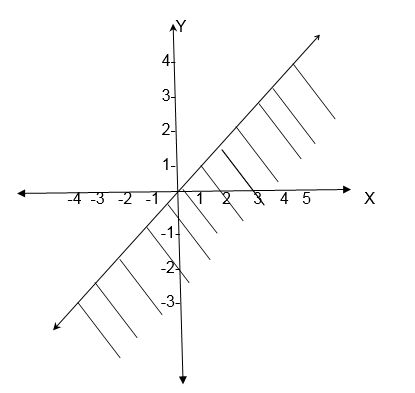
Which of the following ordered pairs belong to the relation {(x, y): y>x}?
(1, 2), (2, 1), (-3, 4), (-3, -5), (2, 2), (-8, 0), (-8, -3).
Solution.
(1, 2), (-3, 4), (-8, 0), (8,-3).
Relations Pictorially
Demonstrate relations pictorially
For example the relation ” is greater than ” involving numbers 1,2,3,4,5 and 6 where 1,3 and 5 belong to set A and 2,4 and 6 belong to set B can be indicate as follows:-
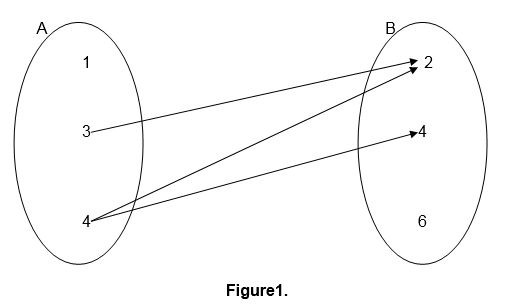
This kind of relation representation is referred to as pictorial representation.
Relations can also be defined in terms of ordered pairs (a,b) for which a is related to b and a is an element of set A while b is an element of set B.

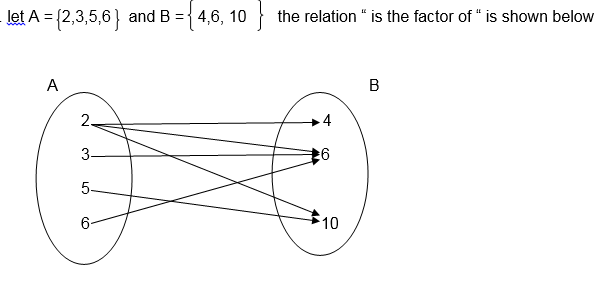
For example the relation ” is a factor of ” for numbers 2,3,5,6,7 and 10 where 2,3,5 and 6 belong to set A and 6,7 and 10 belong to set B can be illustrated as follows:-
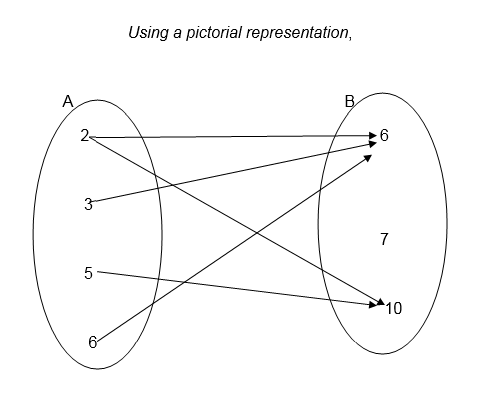

Example 1
1. Draw an arrow diagram to illustrate the relation which connects each element of set A with its square.
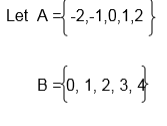
Solution
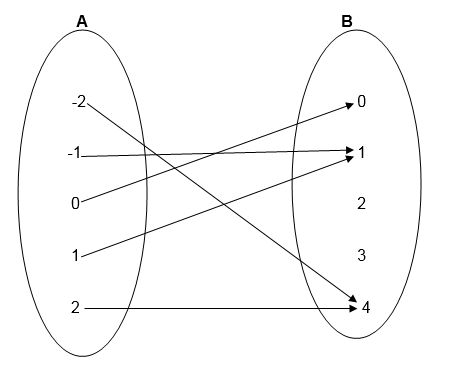
Example 2
Using the information given in example 1, write down the relation in set notation of ordered pairs. List the elements of ordered pairs.

Example 3
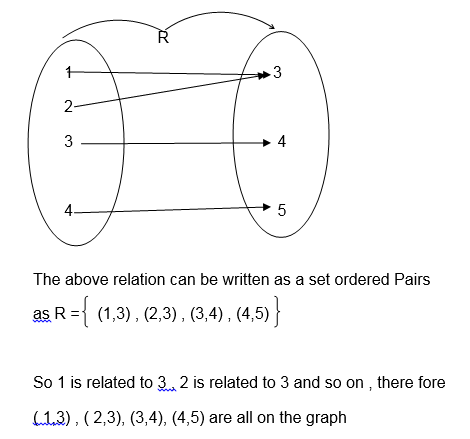
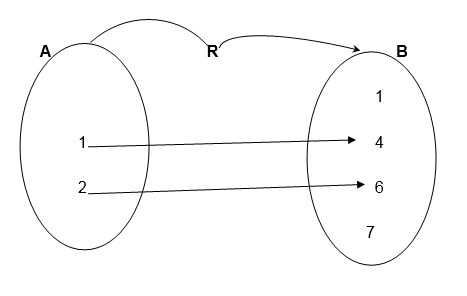
Consider the relation below:

Solution;
Example 4
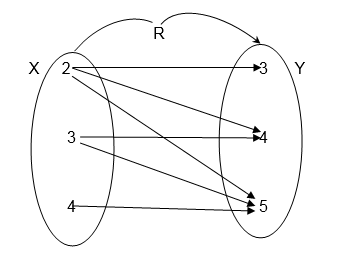
Let X= {2, 3, 4 } and Y= {3 ,4, 5}
Draw an arrow diagram to illustrate the relation ” is less than”
Exercise 1
Let P= {Tanzania, China, Burundi, Nigeria}
Draw a pictorial diagram between P and itself to show the relation
“Has a larger population than”
2. Let A = 9,10,14,12 and B = 2,5,7,9 Draw an arrow diagram between A and B to illustrate the relation ” is a multiple of”
3.Let A = mass, Length, time and
B = {Centimeters, Seconds, Hours, Kilograms, Tones}
Use the set notation of ordered pairs to illustrate the relation “Can be measured in”
4. A group people contain the following; Paul Koko, Alice Juma, Paul Hassan and Musa Koko. Let F be the set of all first names, and S the set of all second names.
Draw an arrow diagram to show the connection between F and S
5. Let R={ (x, y): y=x+2}
Where x∈A and A ={ -1,0,1,2}
and y∈B, List all members of set B
Exercise 2
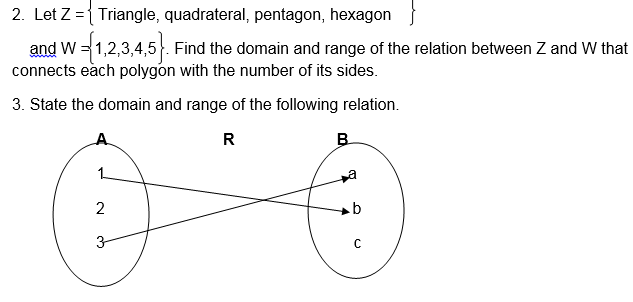
1. Let the relation be defined
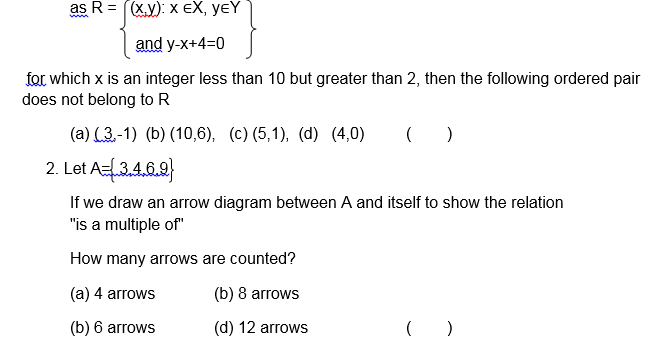
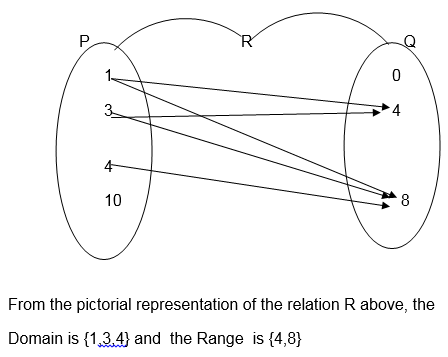
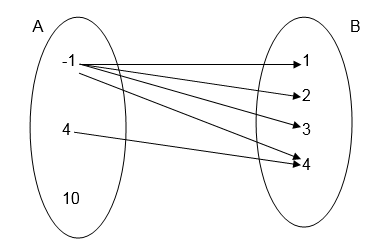
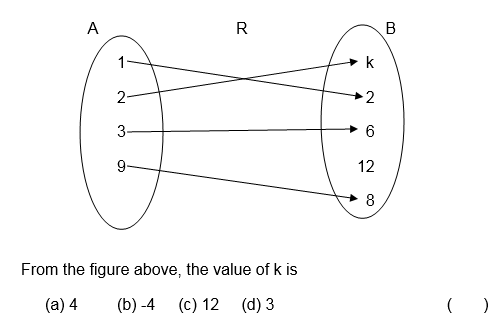
3. Consider the following pictorial diagram representing a relation R.
4. Let the relation R be defined as

5. A relation R on sets a and B where A = 1,2,3,4,5 and B = 7,8,9,10,11,12 is defined as ” is a factor of “

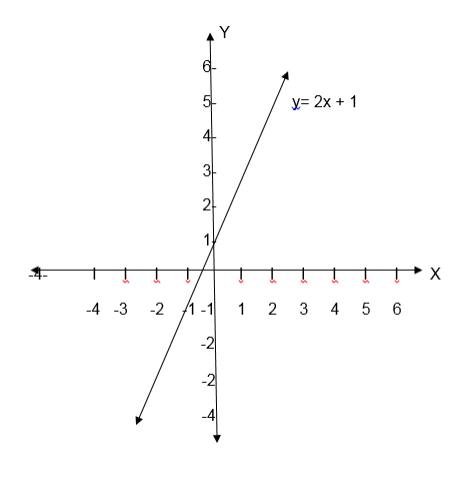
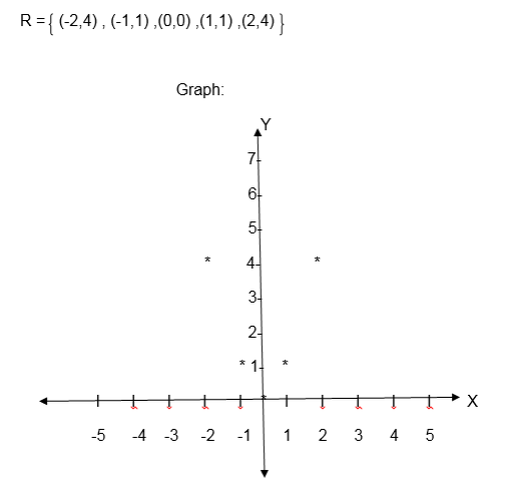
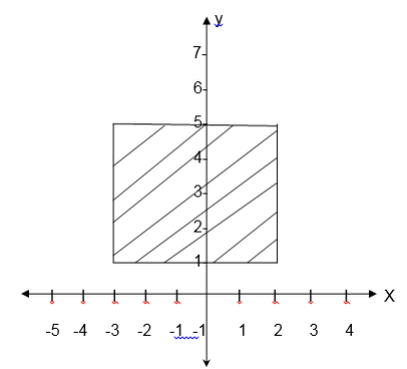
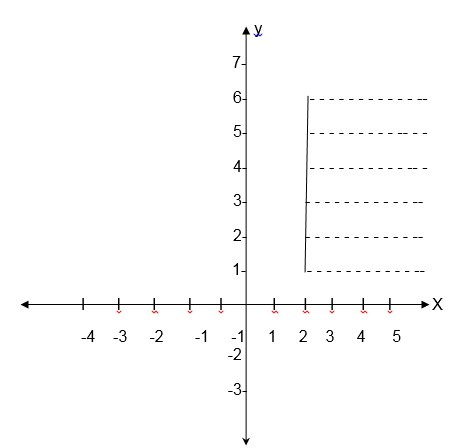
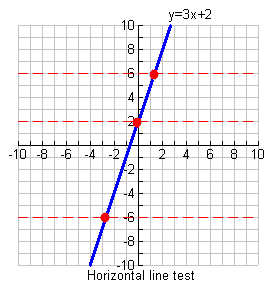
Graph of a Relation
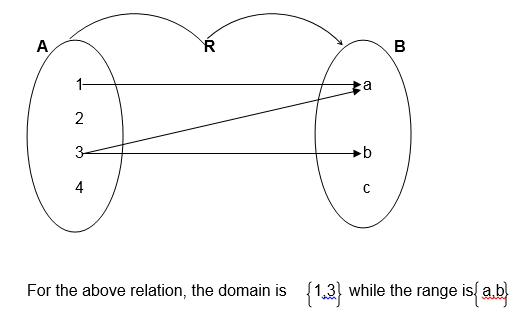
Domain and Range of a Relation
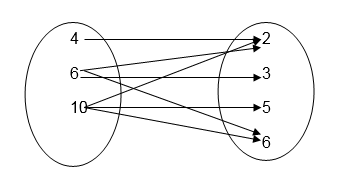
Inverse of a Relation