JOIN US WHATSAPP
CLICK HERE
JOIN US TELEGRAM
CLICK HERE
TOPIC 1: EXPONENTS AND RADICALS


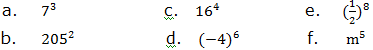
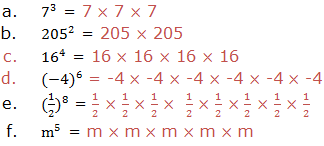
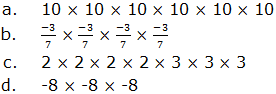
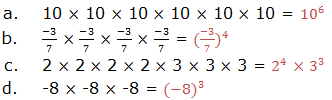
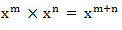
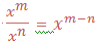
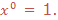
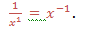
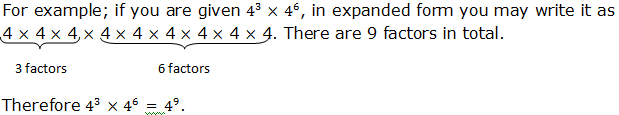
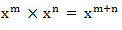
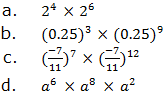
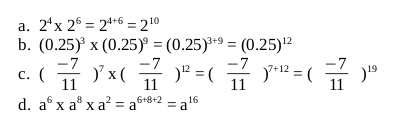
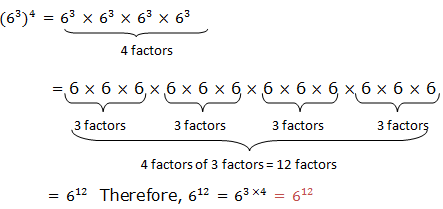
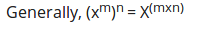
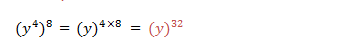
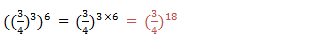
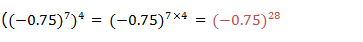
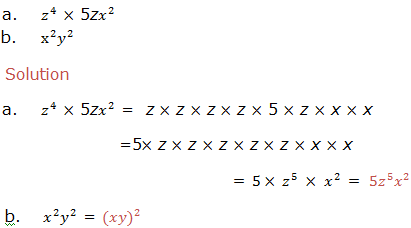
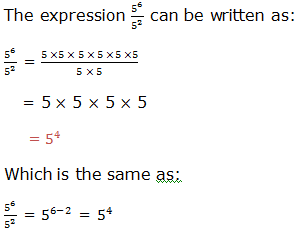
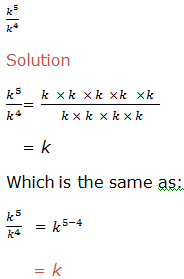
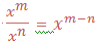
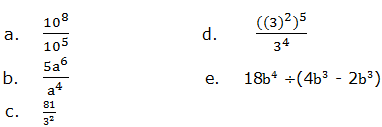
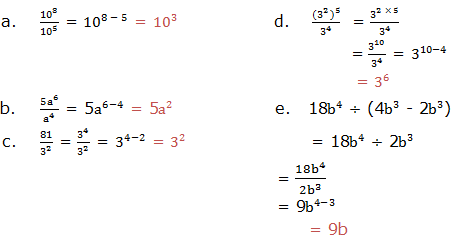
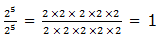
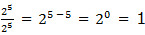
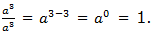
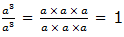


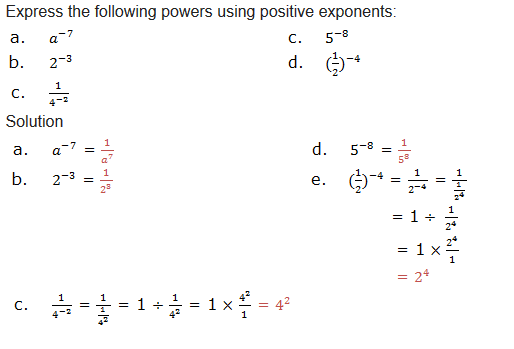



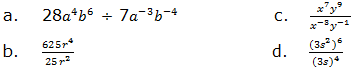
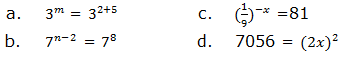
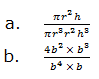


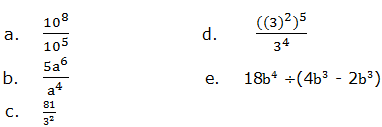
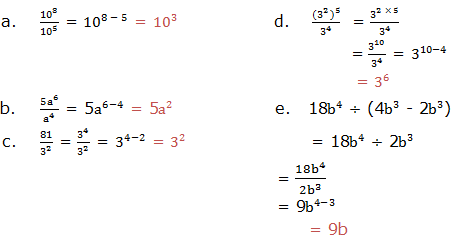
Exponents
Exponents tell how many times to use a number itself in multiplication. There are different laws that guides in calculations involving exponents. In this chapter we are going to see how these laws are used.
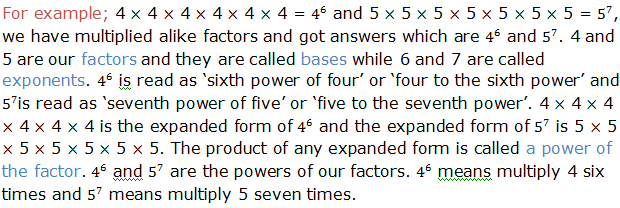
Single exponent tutorial
Tutorial Created by Willbald Mvungi-Ilboru Secondary
Indication of power, base and exponent is done as follows:

Solution:

To write the expanded form of the following powers:
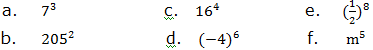
Solution
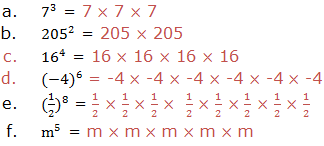
To write each of the following in power form:
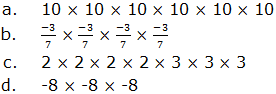
Soln.
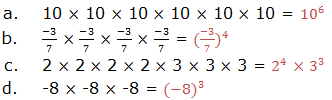
The Laws of Exponents
List the laws of exponents
First law:Multiplication of positive integral exponent
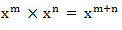
Second law: Division of positive integral exponent
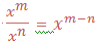
Third law: Zero exponents
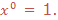
Fourth law: Negative integral exponents
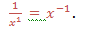
Verification of the Laws of Exponents
Verify the laws of exponents
First law: Multiplication of positive integral exponent
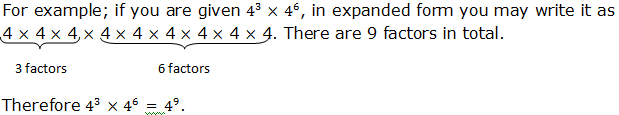
Exponent Multiplication Tutorial
Tutorial Created by Willbald Mvungi-Ilboru Secondary
Generally, when we multiply powers having the same base, we add their exponents. If x is any base and m and n are the exponents, therefore:
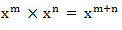
Example 1
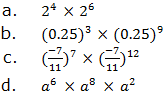
Solution
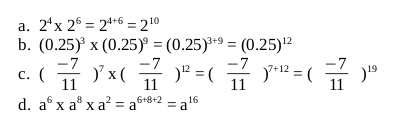
If you are to write the expression using the single exponent, for example,(63)4.The expression can be written in expanded form as:
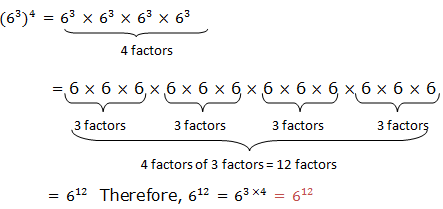
Generally if x is any real number, n and m are integers,
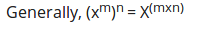
Example 2
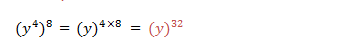
Example 3
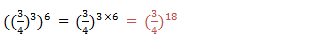
Example 4
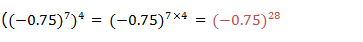
More examples below
Example 5
Rewrite the following expressions under a single exponent for those with identical exponents:
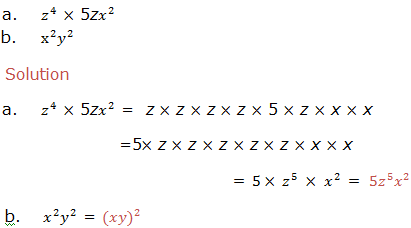
Second law: Division of positive integral exponent
Example 6
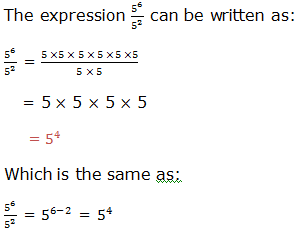
Example 7
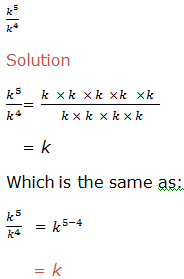
Therefore, to divide powers of the same base we subtract their exponents (subtract the exponent of the divisor from the exponent of the dividend). That is,
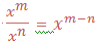
where x is a real number and x ≠ 0, m and n are integers. m is the exponent of the dividend and n is the exponent of the divisor.
Example 8
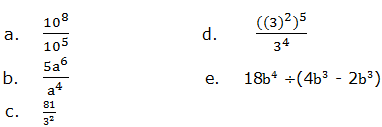
solution
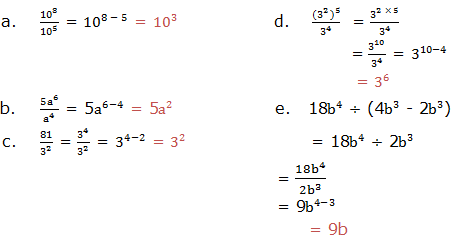
Third law: Zero exponents
Example 9
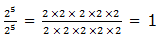
This is the same as:
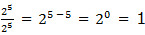
If a ≠ 0, then
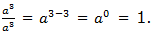
Which is the same as:
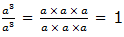
Therefore if x is any real number not equal to zero, then X0 = 1,Note that 00is undefined (not defined).
Fourth law: Negative integral exponents

Also;

Example 10
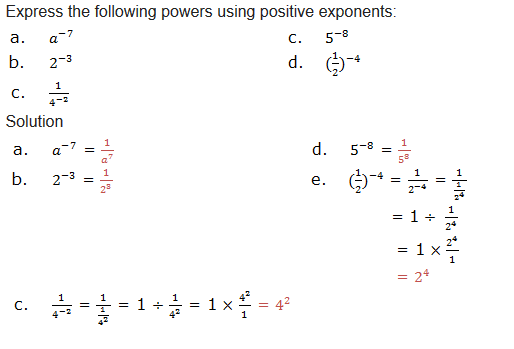
Exercise 1
1. Indicate base and exponent in each of the following expressions:

2. Write each of the following expressions in expanded form:

3. Write in power form each of the following numbers by choosing the smallest base:
- 169
- 81
- 10,000
- 625
a. 169 b. 81c. 10 000 d. 625
4. Write each of the following expressions using a single exponent:

5. Simplify the following expressions:
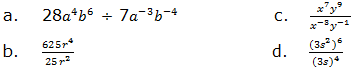
6. Solve the following equations:
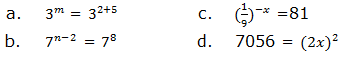
7. Express 64 as a power with:
- Base 4
- Base 8
- Base 2
Base 4 Base 8 Base 2
8. Simplify the following expressions and give your answers in either zero or negative integral exponents.
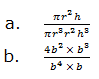
9. Give the product in each of the following:

10. Write the reciprocal of the following numbers:

Laws of Exponents in Computations
Apply laws of exponents in computations
Example 11
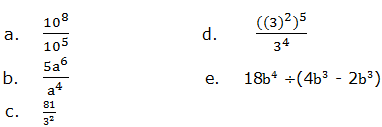
Solution
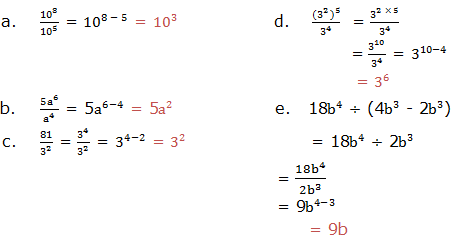
Radicals
Transposition of Formula



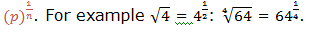


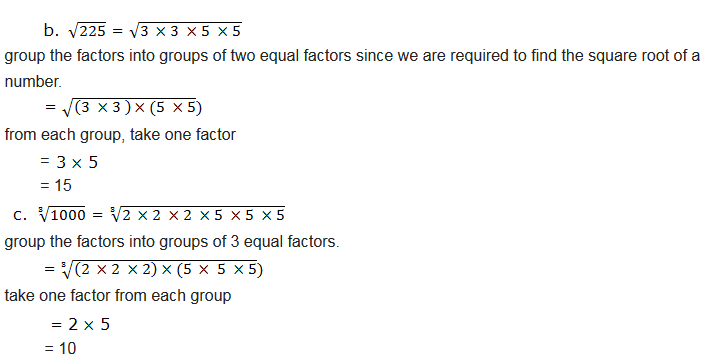
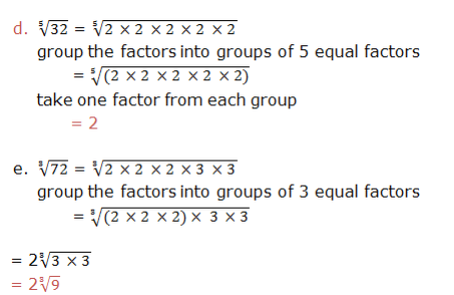
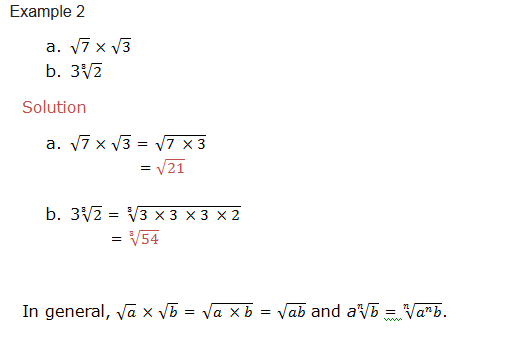
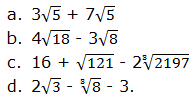
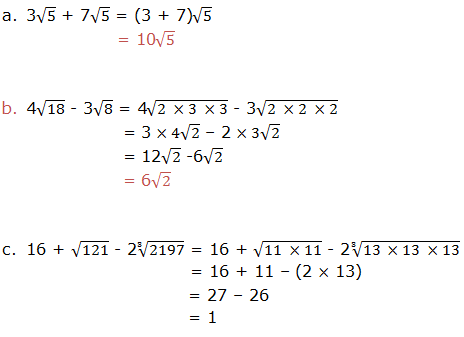
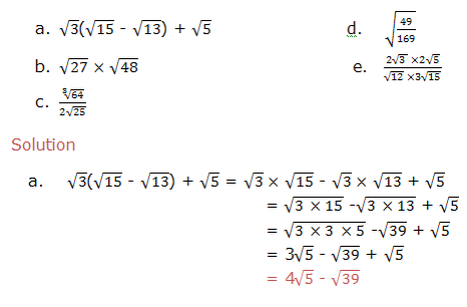
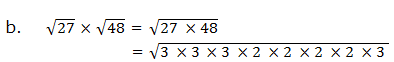
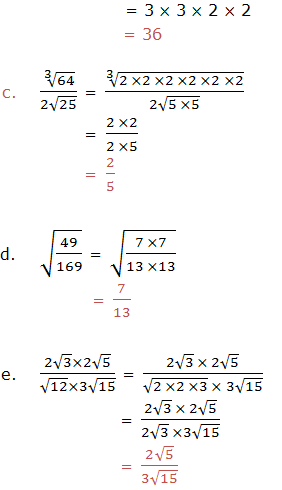



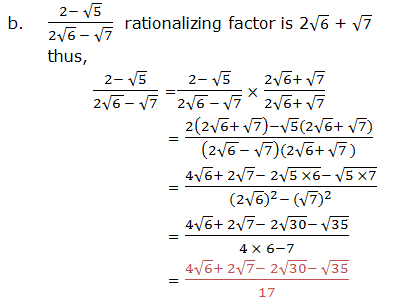





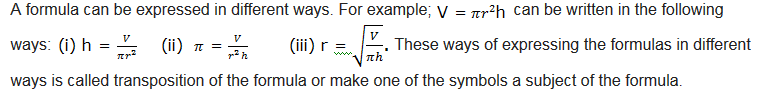


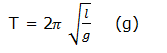
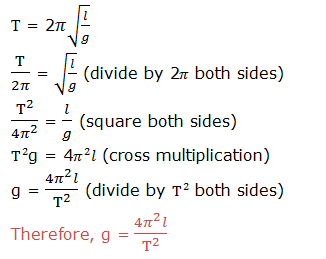



2 Comments
Well and comfortable study
Wow it's so enjoyable