Close Menu
    Button Login
    Clickable WP Image
    Mathematics

    MATHEMATICS: FORM TWO: Topic 7 – GEOMETRIC AND TRANSFORMATIONS

    Msomi BoraBy No Comments10 Mins Read

    TOPIC 7: GEOMETRIC AND TRANSFORMATIONS

    Reflection
    The Characteristics of Reflection in a Plane
    Describe the characteristics of reflection in a plane
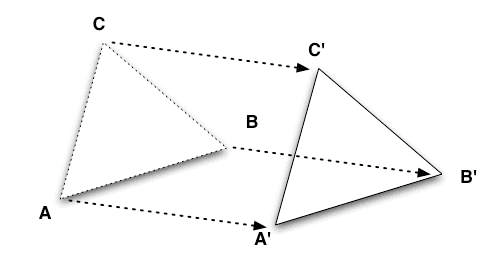
    A transformation in a plane is a mapping which moves an object from one position to another within the plane. Think of a book being taken from one comer of a table to another comer. Figures on a plane of paper can also be shifted to a new position by a transformation. The new position after a transformation is called the image. Examples of transformations are reflection, rotation, enlargement and translation.
    Different Reflections by Drawings
    Represent different reflections by drawings
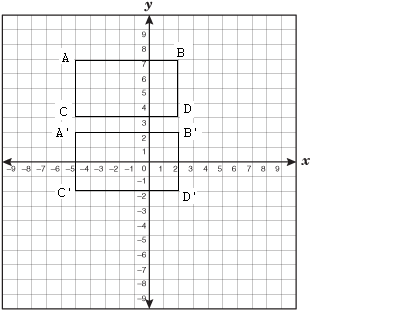
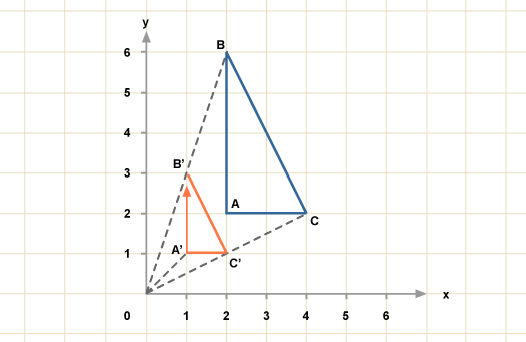
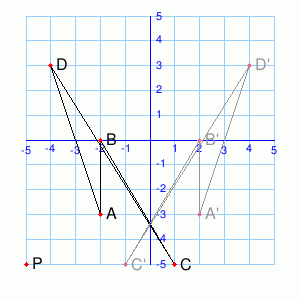
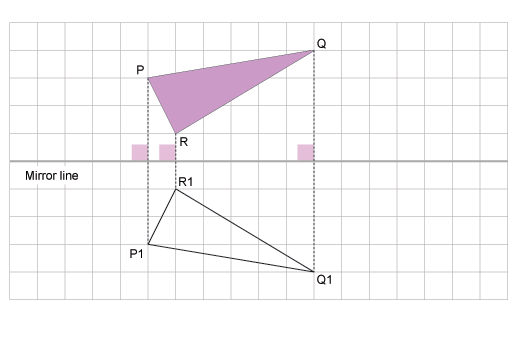
    A reflection is a transformation which reflects all points of a plane in a line called the mirror-line. The image in a mirror is as far behind the mirror as the object is in front of the mirror
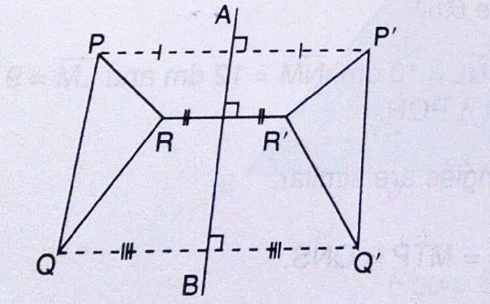
    Characteristics of Reflection
    In the diagram, APQR is mapped onto ΔP’Q’R’ under a reflection in the line AB. If the paper is folded along the line AB, ΔPQR will fall in exactly onto ΔPQR. The line AB is the mirror-line. which is the perpendicular bisector of PP’, QQ’ and ΔPQR and ΔP’Q’R are congruent.
    Some characteristics observed under reflection are:
    1. PP’ is perpendicular to AB, RR’ is perpendicular to AB and QQ is perpendicular to AB.
    2. The image of any point on the Q’ mirror line is the point itself.
    3. PP’ is parallel to RR’ and QQ’
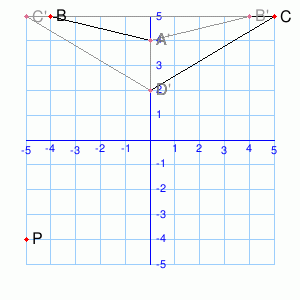
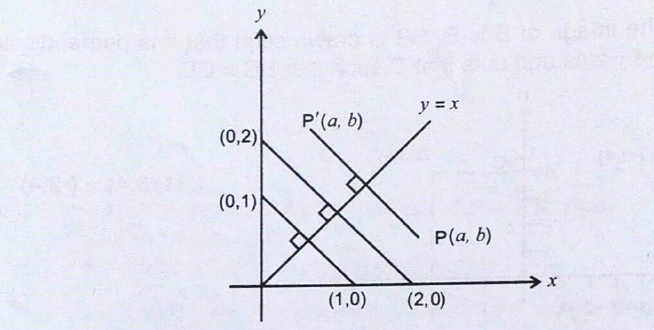
    Reflection in the Line y = x
    The line y = x makes an angle 45° with the x and y axes. It is the line of symmetry for the angle YOX formed by the two axes. By using the isosceles triangle properties, reflection of the point (1, 0) in the line y = x will be (0, 1).
    The reflection of (0,2) in the liney = x will be (2,0). You notice that the co-ordinates are exchanging positions. Generally, the reflection of the point (a,b) in the line y = x is (b,a).
    The reflection of the point B(c,d) in the line y = -x is B’ (-d, -c)
    Tutorial on reflection through y=x
    Tutorial Created by Willbald Mvungi-Ilboru Secondary
    Exercise 1
    1. Find the image of the point D(4,2) under a reflection in the x-axis.
    2. Find the image of the point P(-2,5) under a reflection in the x-axis.
    3. Point Q(-4,3) is reflected in the y-axis. Find the coordinates of its image.
    4. Point R(6,-5) is reflected in the y-axis. Find the co-ordinates of its image.
    5. Reflect the point (1 ,2) in the line y = -x.
    6. Reflect the point (5,3) in the line y = x.
    7. Find the image of the point (1 ,2) after a reflection in the line y=x followed by another reflection in the line y = -x.
    8. Find the image of the point P(-2,1) in the line y = -x followed by another reflection in the line x = 0 ketch the positions of the image P and the point P, indicating clearly the lines involved.
    9. Find the co-ordinates of the image of the point A(5,2) under a reflection in the line y = 0.
    10. Find the coordinates of the image of the point under a reflection in the line x = 0.
    11. The co-ordinates of the image of a point R reflected in the x axis is R(2, -9). Find the coordinates of R.
    Rotations
    Characteristics of a Rotation on a Plane
    Describe characteristics of a rotation on a plane
    Rotation is a transformation which rotates all points on a plane about a fixed point known as the centre of rotation through a given angle in a clockwise or anticlockwise direction
    In order to describe a rotation, we give:
    1. the centre of rotation,
    2. the angle of rotation, and
    3. the direction of rotation
    Example 1
    Copy the figure T and rotate 180° about the origin.
    Different Rotation on a Plane by Drawings
    Represent different rotation on a plane by drawings
    When you turn a ruler at its end corner through an angle 0° it make a rotation. A rotation is transformation which moves a point through a given angle about a fixed point.
    A rotation is a transformation that turns a figure about a fixed point called a Centre of Rotation.You can rotate the figure as much as 360 degrees. The transformation of Rotation is usually denoted by R. The symbol R› means that an object is rotated through an angle 9. In the xy plane, when is measured in the clockwise direction it is negative and when it is measured in the anticlockwise direction it is positive.
    P is on the x-axis
    After a rotation through 90° about the origin it will be on the y-axis. Since P is 1 from O, P’ is 1 from O, the coordinates of P are P'(O,I). Hence R90°( 1, O) = (O, 1)
    Exercise 2
    1. Find the image of the point (1, 2) under a rotation through 180° anti-clockwise about the origin.
    2. Find the rotation of the point (6, 0) under a rotation through 90° Clockwise about the origin.
    3. Find the rotation of the point (-2, 1) under a rotation through 270° clockwise about the origin.
    4. Point Q(5, -4) is rotated through 270° in the clockwise direction. Find the coordinates of its image.
    5. Find the image of (1, 2) after a rotation of -90°
    6. Find the image of (-3, 5) after a rotation of -180°
    7. Find the image of (-5, 0) after a rotation of -180°
    8. Find the image of (-5, 0) after a rotation of 180° about the origin. Comment about the results of questions 7 and 8.
    9. The vertices of triangle OAB are O(0,0), A(2,3) and B(2,1). The triangle is rotated through 90° anti-clockwise about the origin. Find the co-ordinates of its image.
    10. The vertices of rectangle PQRS are P(0,0), Q(3,0), R(2,3), S(0,2). The rectangle is rotated through 90° clockwise about the origin. a) Find the co-ordinates of its image b) draw the image.
    Translation
    Properties of Translations
    State properties of translations
    Translation is a transformation which moves all points, on a plane through the same direction
    In the diagram, ΔABC slidesΔA’B’C’ (A’ is read as A prime) is the direction AA’. Note that AA’ are parallel and of equal length. We say that ABC is mapped onto A’B’C’ by a translation.
    A translation usually denoted by T. For example 1(1, 1) = (6, 1) means that the point 1(1,1) has been moved to (6, 1) by a translation T. This translation will move theorigin (0,0) to (5,0) and is written as T = 5/0.
    Translations Drawings
    Represent translations drawings
    Translation drawings
    If you cast a shadow of an object onto a plane surface, say a wall, by using a light source, the shadow becomes bigger as the object moves closer to the light source.
    In figure 7.40, AB casts a shadow CD. When AB moves to a new position and is renamed QP (same size with AB) the shadow of QP becomes SR and it is greater than CD.
    Enlargement
    A Scale of Enlargement
    Develop a scale of enlargement
    Tutorial on Enlargement
    Tutorial Created by Willbald Mvungi-Ilboru Secondary
    Enlargement is a transformation in which a figure is made larger (magnified) or made smaller (diminished). A photograph may be enlarged or diminished to suit a Certain purpose. Figures can be drawn to scale where actual figures are diminished or enlarged. Enlarged shapes are geometrically similar and have corresponding angles equal. The number that magnifies or diminishes a figure is called the enlargement factor and is usually denoted by k. If k is less than 1 the figure is diminished and if it is greater that 1 the figure is enlarged k times.
    In the case of closed figures, if the lengths enlarged by a factor of k then the area is enlarged by k2.
    Scale
    Similarity can be used in enlarging of diminishing geometrical figures. For example in maps, a large area of land is represented by a small area on paper by a scale. Scale is a ratio between the measurement of a drawing to the actual measurement. It is normally stated in the form of 1 : n, for example, if a scale of a map is 1.20000, then 1 unit on the map represents 20000 units on the ground.
    In the figure, triangle ABC is a scale measurement of triangle PQR, where the scale is 1:2.
    Scale is measurement of drawing: Actual Measurement, that is,
    Scale = Measurement of drawing/Actual measurement
    Exercise 3
    Find the length of a drawing that represents:
    1. 15 km when the scale is 1:500000
    2. 45 km when the scale is 1 km to 900 m.
    A building2 50 metres high is representedb y a line segment of length 5 cm. Finc the scale of the drawing.
    A triangular plot of land has sides 152 metres and 208 metres meeting at an angle of 500. Find by scale drawing the distance from the middle point of the longest side to the opposite corner
    Enlargement of a Given Figures
    Construct enlargement of a given figures
    Consider two similar rectangles shown in the figure below with a scale factor k.
    If AB = a and AD = a, then PO = ak and PS bk
    Area of ABCD = a× a = ab
    Area of PORS = ak x bk = abk2
    Area of PORS/Area of ABCD = abk2/ab = k2
    Therefore, if two polygons have a scale factor k then the ratio of their areas is k2. This is also called the scale factor for the area.
    Figures to Scale
    Draw figures to scale
    If we ‘enlarge’ a shape by a scale factor that is between -1 and 1, the image will besmallerthan the object
    Example 2
    Enlarge triangleABCwith a scale factor1/2, centred about the origin.
    Solution
    The scale factor is1/2, so:
    OA’ =1/2OA
    OB’ =1/2OB
    OC’ =1/2OC
    Since the centre is the origin, we can in this case multiply each coordinate by1/2to get the answers.
    A = (2, 2), so A’ will be (1, 1).
    B = (2, 6), so B’ will be (1, 3).
    C = (4, 2), so C’ will be (2, 1).
    Actual Distances Represented by a Scale Drawings
    Find actual distances represented by a scale drawings
    If two polygons are similar and the ratio of their corresponding sides of two similar polygons is 5:3, then the scale of enlargement is 5/3
    Exercise 4
    1. Two triangles are similar but not congruent. Is one the enlargement of the other?
    2. The length of a rectangle is twice the length of another rectangle. Is one necessarily an enlargement of the other? Explain.
    3. In the figure below BC DE, AB 5 cm, BD = 3cm and EF = 4 cm
    1. State which triangle is an enlargement of ΔABC
    2. Calculate the scale factor of the enlargement.
    Combined Transformations
    Combined Transformations
    Draw combined transformations
    Combined transformation tutorial
    Tutorial by Willbald Mvungi from ILBORU
    Combined Transformation means that two or more transformations will be Performed on one object. For instance you could perform a reflection and then a translation on the same point
    Example 3
    What type of transform takes ABCD to A’B’C’D’?
    Solution
    The type of transform takes ABCD to A’B’C’D’ is Reflection
    Simple Problems on Combined Transformations
    Solve simple problems on combined transformations
    Exercise 5
    What type of transform takes ABCD to A’B’C’D’?
    The transformation ABCD → A’B’C’D’ is a rotation around(-1, 2)by___°.Rotate P around(-1, 2)by the same angle. (You may need to sketch things out on paper.)P’ = (__,__)
    The transformation ABCD → A’B’C’D’ is a rotation around(-1, -3)by__°Rotate P around(-1, -3)by the same angle. (You may need to sketch things out on paper.)P’ = (__,__)
    Share.

    Related Posts

    Leave A Reply

    error: Content is protected !!
    Verified by MonsterInsights