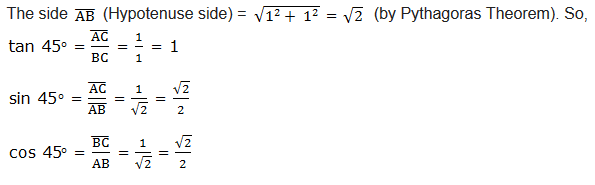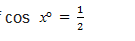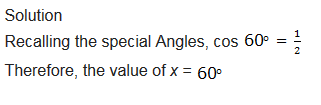JOIN US WHATSAPP
CLICK HERE
JOIN US TELEGRAM
CLICK HERE
TOPIC 9: TRIGONOMETRY
Do you want to learn the relationships involving lengths and Angles of right-angled triangle? Here, is where you can learn.
Trigonometric Rations
Trigonometry is all about Triangles. In this chapter we are going to deal with Right Angled Triangle. Consider the Right Angled triangle below:
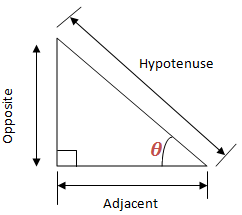
The sides are given names according to their properties relating to the Angle .
Adjacent side is adjacent (next to) to the Angle
Opposite side is opposite the Angle
Hypotenuse side is the longest side
Sine, Cosine and Tangent of an Angle using a Right Angled Triangle
Define sine, cosine and tangent of an angle using a right angled triangle
Trigonometry is good at finding the missing side or Angle of a right angled triangle. The special functions, sine, cosine and tangent help us. They are simply one of a triangle divide by another. See similar triangles below:
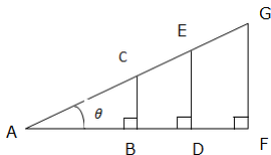
The ratios of the corresponding sides are:
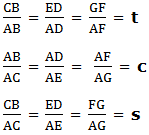
Where by t, c and s are constant ratios called tangent (t), cosine (c) and sine (s) of Angle respectively.
The right-angled triangle can be used to define trigonometrical ratios as follows:
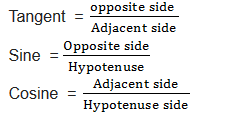
The short form of Tangent is tan, that of sine is sin and that of Cosine is cos.
The simple way to remember the definition of sine, cosine and tangent is the word SOHCAHTOA. This means sine is Opposite (O) over Hypotenuse (H); cosine is Adjacent (A) over Hypotenuse (H); and tangent is Opposite (O) over Adjacent (A). Or

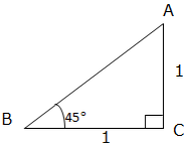
Example 1
Given a triangle below, find sine, cosine and Tangent of an angle indicated.
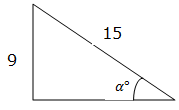
Solution

Example 2
Given that
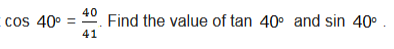

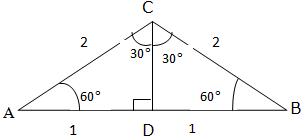
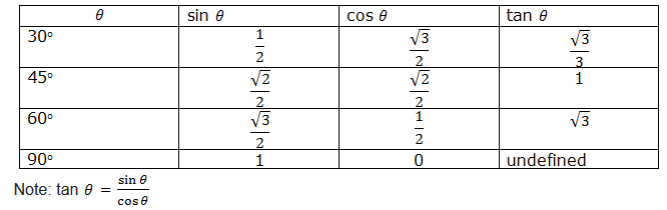
Trigonometric Ratios of Special Angles
Trigonometric Tables
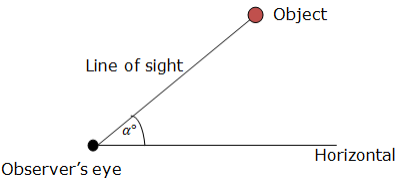
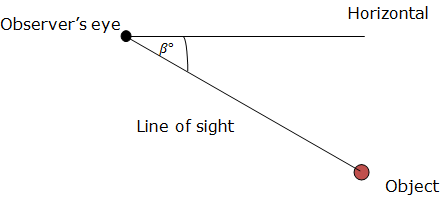
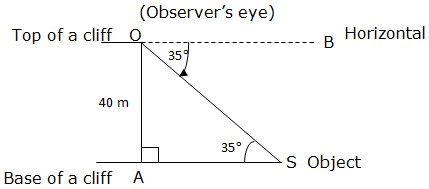
Angles of Elevation and Depression