Close Menu
    Button Login
    Clickable WP Image
    Physics

    PHYSICS: FORM ONE: Topic 5 – ARCHIMEDES’ PRINCIPLE AND LAW OF FLOTATION

    Msomi BoraBy No Comments12 Mins Read


    TOPIC 5: ARCHIMEDES’ PRINCIPLE AND LAW OF FLOTATION

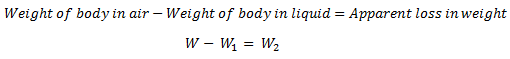
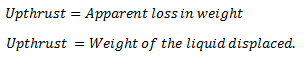
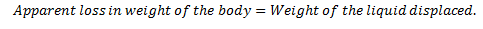
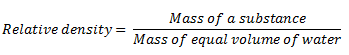
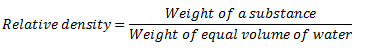
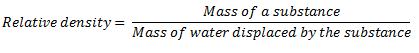
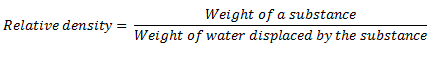
    Archimedes’ Principle
    Archimedes’ principle indicates that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially submerged, is equal to the weight of the fluid that the body displaces.
    The Concept of Upthrust
    Explain the concept of upthrust
    If a heavy object is lifted while immersed in water, it may be raised more easily than when outside the water. This is due to the reason that when anything is placed in liquid, it receives an upward force called upthrust. A body appears to have lost some weight when immersed in water due to the upthrust exerted on the body by the water.
    • By definition upthrust is referred as an upward force exerted by the body when it’s partially or totally immersed in water.
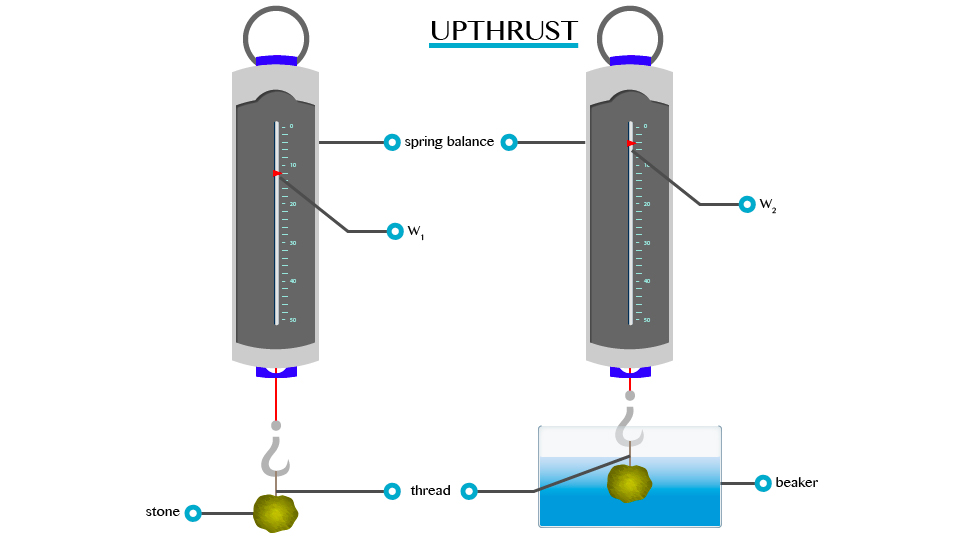
    • Consider the experiment below to verity the concept of upthrust.
    From this experiment, it will be observed that W1>W2. This is because:
    When a body is partially or totally immersed in any liquid, the liquid exerts an upward force.
    A weight recorded on the spring balance of a body that is totally or partially immersed in any liquid is called apparent weight. E.g. W2 and the force, which temporally reduces the weight of the body, are called upthrust (u).
    Verification of the Archimedes’ Principle
    Verify the archimedes principle
    The Archimedes’ principle describes about two important things.
    • A body immersed in a fluid experiences forces one of them is up-thrust
    • The weight of the fluid displaced is equal to the up-thrust.
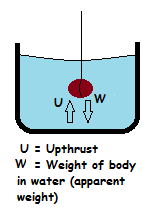
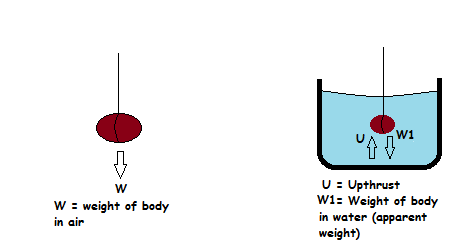
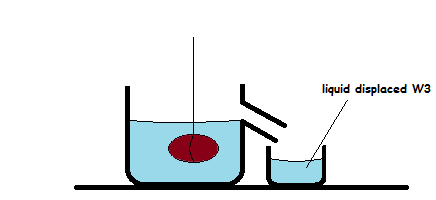
    The forces acting on a body in air and when immersed in a liquid can be shown in following diagrams;
    When a body is immersed in a liquid it experiences an upward force from the liquid. This force is known as up-thrust. Up-thrust opposes the weight of the body.
    Since the weight of the body is opposed by the up-thrust, it follows that the weight of the body when in the liquid (W1) is decreased and become smaller than the weight of the body in air (W).
    The differences between weight of the body in air and the weight of the body in the liquid (Apparent weight) is known as Apparent loss in weight (W2).
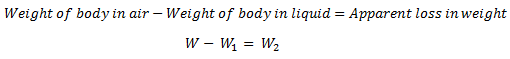
    This apparent loss in weight (W2) is equal to the weight of the liquid which is displaced after immersing the body.
    Therefore,
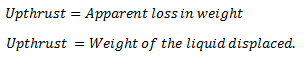
    Hence it can be shown that,
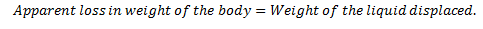
    Activity 1
    Aim; Aim of this activity is to verify Archimedes’ principle.
    Apparatus;
    • Spring balance
    • Digital /beam balance
    • 1 beaker
    • Eureka can
    • water
    • 1 piece of small stone
    • A cotton thread a string
    Procedure;
    • Measure the weight of empty beaker (Wb) using beam/ digital balance.
    • Fill the eureka can with water until water to starts to fall out of its beak.
    • Attach the stone to the spring balance to measure its weight by using a cotton thread /string.
    • Record the weight of stone in air as W.
    • Place the empty beaker under the beak of the Eureka can.
    • Slowly immerse the stone in the water and observe the changes the readings of the spring balance.
    • Water will be displaced and collected by the beaker.
    • Record the apparent weight of the stone (weight of the stone in water) as W1.
    • Put the beaker with displaced water on the digital balance to measure the weight of the beaker +water =Wbw .
    Discussion;
    • Weight of the water displaced (Ww) can be obtained by taking (weight of beaker + weight of displaced water) –weight of empty beaker=WbwWb. Ww=Wbw-Wb
    • Apparent loss in weight (W2) of the store can be obtained by taking weight of store in air –Apparent weight =W-W1
    Questions;
    1. Are the values Ww and W2 equal?
    2. What is the Upthrust experienced by the stone?
    Example 1
    Weight of a body in air = 10.0N
    Weight of a body when immersed in water = 9.2N find the upthrust.
    Solution:
    Data given
    Weight of a body in air (W1)= 10.0N
    Weight of a body when in water (W2) = 9.2N
    Formula
    Upthrust = Loss of weight in water = W1-W2
    = 10.0N – 9.2N
    = 0.8N
    The upthrust is 0.8
    Example 2
    The weight of a body when totally immersed in liquid is 4.2N. if the weight of the liquid displaced is 2.5N, find the weight of the body in the air.
    Solution;
    Data;
    Apparent weight (W2) = 4.2N
    Weight of liquid displaced (u) = 2.5N
    Weight of body in air=?
    Formular;
    U = W1 –W2
    W1= 4.2 +2.5 = 6.7N
    Weight of body in air is 6.7N
    The Archimedes’ Principle in Determining Relative Density
    Apply the archimedes principle to determine relative density
    Relative density (R.D) of a substance can be defined as the ratio of the mass of a substance to the mass of an equal volume of water.
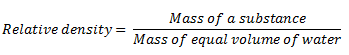
    Relative density can also be defined as the ratio of the weight of the substance to the weight of an equal volume of water.
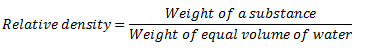
    According to Archimedes’ principle mass of equal volume of water is the mass of the water displaced when the substance is immersed in water.
    Note that, the volume of water displaced after immersing a substance in water is equal to the volume of the substance.
    That means,
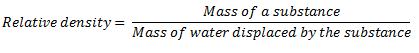
    Or,
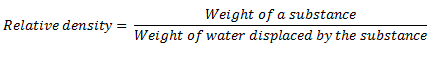
    Example 3
    A piece of glass weigh 1.2N in air and 0.7N when completely immersed water. Calculate its:
    1. Relative density
    2. Density of a glass
    Given that density of water = 1000kg/cm3
    And acceleration due to gravity = 10N/kg
    Solution
    Weight of the glass in air (W1) = 1.2N
    Weight of the glass in water (W2) = 0.7N
    R.D = W1/W1 – W2
    1.2N/(1.2 – 0.7)
    1.2/0.5
    R.D = 2.4
    R.D = Density of glass/Density of water
    Density of a glass = R.D x Density of water
    = 2.4 x 1000kg/cm
    = 2400kg/m3
    NB: Relative density has no SI unit
    Law of Flotation
    Difference between Floating and Sinking of Objects
    Distinguish floating and sinking of objects
    As we have discussed in upthrust, different objects with different density can sink or float. The object with higher density than water density will sink while that object with a density lower than water’s density will float. For example, a coin sinks in water and a large ship floats on water.
    A bowl placed on the surface of water will stay on the surface or on top of water.
    This tendency of the body to remain on the surface of the fluid is known as floating.
    On the other hand, a metal block such as steel block when placed on water will descend to the bottom of the container.
    This tendency of an object to drop to the bottom of the liquid is known sinking.
    The following table shows differences between floating and sinking
    Floating Sinking
    1. The body stays at the surface of the liquid. The body drop to the bottom of the liquid.
    2. Takes place when the upward force (up-thrust) is greater than the weight of the body. Takes place when the up-thrust on the object is smaller than the weight of the body.
    3. Takes place when density of the body is less than density of the liquid. Takes place when the density of the body is greater than density of the liquid.
    The Conditions for a Substance to Float in Fluids
    Explain the conditions for a substance to float in fluids
    When an object is completely or partially immersed in fluids, there are two forces acting on it, the weight (W) acting downwards and the upstrust (u) acting upwards. Refer to the figure below:
    The following conditions can be used to determine the position of the object in the fluid.
    1. If W>U, there is downward movement of the body which is termed as sinking.
    2. If W<U, there is upward movement of the body.
    3. If W=U, the body is equilibrium under the action of two equal and opposite force. Thus, the body floats.
    The buoyant force(upthrust) depends on the volume of the object and the density of the surrounding fluid.
    For example;
    • The greater the volume of the object, the greater the possibility of floating. A ship floats on the sea because it has a hollow space inside it which increases its volume. Also, a coin sinks in sea because it has smaller volume. The large volume of the object makes the object to displace more fluid hence increasing the upthrust on it and cause it to float.
    • The greater the density of the surrounding fluid, the greater the possibility of the object to float. It is easier for a solid to float in honey or glycerin than in water because honey and glycerin have large density than water. That means, the greater the density of the surrounding, the greater is the buoyant force.
    The following are the conditions for the body to float in fluid;
    1. The volume of the body must be larger so as to displace large amount of fluid.
    2. The density of the body must be smaller than the density of the surrounding fluid.
    3. The upthrust (buoyant force) due to surrounding fluid must be equal to the total weight of the body.
    Relationship between Upthrust and Weight of Floating Body
    Relate upthrust and weight of floating body
    Upthrust and flotation are well related through the density of the object and the density of the surrounding fluid. For the body to float in the fluid, the upthrust must be controlled. Upthrust is controlled by controlling the density of the object and the density of the surrounding fluid.
    The object will float if the density of the body is less than the density of the fluid.
    The density of the object is decreased by increasing the volume of the object.
    However, when a body floats, its weight decreases to zero (weightless). That is why it is very easy to lift or move the object when it is floating in the fluid.
    Principle of Floatation
    State the law of flotation
    The above experiment shows that, the upthrust is equal to the weight of the liquid displaced and therefore the upthrust is equal to the weight of the floating body as the two forces are equal.
    The mass of the floating body is equal to the mass of fluid displaced; in the above experiment is the same as the weight of the piece of wood. This result is agreement with the principle of floatation.
    The principle of floatation states “A floating body displaces a weight of the fluid which is equal to its own weight.”
    The Law of Floatation in Everyday Life
    Apply the law of flotation in everyday life
    Floating of ship
    Iron is much denser than water and a block of iron sinks immediately in water. Ships are made with hollowness such that their total densities are less than that of water. Therefore, a ship displaces water equal to its weights.
    The upthrust of the water is sufficient to support the weight of the ship. When the ship is loaded with cargo it sinks lower in the water. The volume of water displaced by the ship and its cargo depends upon whether it is floating in fresh water or in seawater. It floats lower in fresh water (R.D= 1.0) than in seawater (R.D=1.025) the mass of fresh water displaced.
    For example, if a ship weighs 20,000 tons, then it must displace 20,000 tones of water to float. If 2,000 tones of cargo is added, the ship lowers in water until an extra 1,000 tons of water have been displaced
    Plimsoll line;This line indicates the safe limit of loading. Many plimsoll lines may be marked on a ship to show minimum heights above different types of water in different seasons.
    Balloons
    Figure below shows the type of balloons used to carry instruments to a high altitude for recording meteorological measurements when filled with gas. E.g. helium, it displaces a volume of air equal to its volume.
    Air has greater density compared to the density of a gas in the balloon. Therefore, the weight of air displaced is greater than that of balloon. The balloon drifts up by a force, which is equal to the difference between the upthrust and the total weight of the balloon (W).
    Submarine
    The buoyancy of a submarine depends on the quantity of water in its ballast tanks. When it is required to drive, water is admitted to special tanks. When the water is ejected from the tanks by means of compressed air, the submarine raises to the surface and floats just like any other ship.
    The mode of Action of a Hydrometer
    Describe the mode of action of a Hydrometer
    A hydrometer is an instrument used for measuring the densities of liquids such as milk, alcohol and acids. The greater the density of the liquid the shorter the stem of hydrometer immersed. Hydrometer sinks lower in kerosene and floats higher in water.
    Construction of a Simple Hydrometer
    Construct a simple Hydrometer
    Single hydrometer can be made using pieces of straws or test tubes weighed down with wax.
    Hydrometer in Determining the Relative Density of Different Liquids
    Use Hydrometer to determine the relative density of different liquids
    The relative density of liquid is measured directly by using a suitable hydrometer, it contains:
    1. A heavy sinker, containing mercury or lead shots that keep the hydrometer upright when it floats.
    2. An air bulb to increase the volume of displaced liquid, and overcomes the weight of the sinker.
    3. The stem is thin so that small changes in density give large differences in readings.
    4. The hydrometer is made up of glass so it does not soak up liquids.
    Share.

    Related Posts

    Leave A Reply

    error: Content is protected !!
    Verified by MonsterInsights